打字猴:1.70105006e+09

1701050060

1701050061

1701050062 则g连续，且于是零伦，矛盾．

1701050063

1701050064 （（1）和（2）也可用（3）的方法证．）

1701050065

1701050066

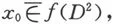
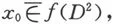
1701050067

1701050068

1701050069 9．用反证法．如果存在则于是D2｛x0｝以S1为收缩核．记r为一收缩映射，则rf∶D2→S1是收缩映射．这与S1不单连通相矛盾．

1701050070

1701050071 10．方法一　记X1是X中第3个坐标不小于0的点的集合，X2是第3个坐标不大于0的点的集合．则X＝X1∪X2，X1，X2都单连通，并且X1∩X2道路连通．用Van-Kampen定理，得X单连通．

1701050072

1701050073

1701050074 方法二　用Van-Kampen定理不难得到下面结论：对任何两个整数单连通．

1701050075

1701050076

1701050077

1701050078

1701050079 以原点O为基点，证明π1（X，O）平凡．证法如下：任取O点处的闭路a，则a（I）是X上的紧致集，从而存在整数k＜l，使得于是a在上定端同伦于O处的点道路，从而a在X上也定端同伦于O处的点道路．

1701050080

1701050081 第　五　章

1701050082

1701050083 §1

1701050084

1701050085 1．设W是E的开集，b∈p（W），取e∈W，使得p（e）＝b．要证b是p（W）的内点．

1701050086

1701050087 取b的一个基本邻域U．设Vα是p-1（U）的包含e点的分支，则同胚p｜Vα∶Vα→U把E的开集W∩Vα映为U的一个包含b点的开集，从而p（W∩Vα）也是b在B中的开邻域，并且它在p（W）中．于是b为p（W）的内点．

1701050088

1701050089 2．若U是一个基本邻域，则∀b∈U，＃p-1（b）等于p-1（U）的分支数．从而同一基本邻域内的诸点的纤维有相同的势．取定b0∈B，记A＝｛b∈B｜＃p-1（b）＝＃p-1（b0）｝，则用上面的结果可以说明A是开集，并且Ac也是开集．由于B连通，又A非空（至少b0∈A），从而A＝B．

1701050090

1701050091 3．要证∀e∈h（U）都是h（U）的内点．设Ub是b＝p（e）一个道路连通的基本邻域，并且Ub⊂U．记Vα是p-1（Ub）的包含e的分支，则Vα是E的开集，并且（p｜Vα）-1∶Vb→Vα在Ub上与h重合（利用定理5.1）．于是Vα＝h（Ub）⊂h（U），从而e是h（Ub）的内点．

1701050092

1701050093 4．设W是X的一个开集，要证p（W）是X/f的开集．∀y∈p（W），设y＝p（x），x∈W．取x的开邻域V，使得V，f（V），…，fn－1（V）两两不相交，并且V⊂W．于是p（V）是含于p（W）的开集，且含y，从而y是p（W）的内点．

1701050094

1701050095 7．F/f可看作F的一半把边界圆周的对径点粘合而得商空间，也即T2上安一个交叉帽，因此是3P2型曲面．

1701050096

1701050097 8．不是．S1上点ei2πα和ei2πb没有基本邻域．

1701050098

1701050099 9．同第8题．

1701050100

1701050101