1701047640
基础拓扑学讲义 [:1701040238]
1701047641
基础拓扑学讲义 第八章 映射度与不动点
1701047642
1701047643
拓扑不变性与同伦不变性使得同调群有广泛的应用,例如第四章中基本群应用的那些例子都可改用1维同调群.由于我们规定了各种维数的同调群,不仅能用它们解决低维的问题(如同基本群),也可解决高维问题,下面列出几个比较直接的应用.
1701047644
1701047645
(1)∀n≥0,Sn不可缩,即与单点空间不同伦.
1701047646
1701047647


1701047648
n=0显然;n>0时,而Hn({p})=0.
1701047649
1701047650


1701047651
(2)当n≠m时,
1701047652
1701047653


1701047654
设n>m,则而Hn(Sm)=0.
1701047655
1701047656


1701047657
(3)当n≠m时,
1701047658
1701047659


1701047660
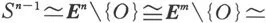
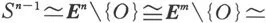
1701047661


1701047662
否则,从而与(2)的结论矛盾.
1701047663
1701047664


1701047665
(4)
1701047666
1701047667


1701047668
(5)在O处没有同胚于En的开邻域,从而n维流形的边界点与内点的区分是有意义的.
1701047669
1701047670
(4)和(5)可仿照第四章中关于n=2的相应情形进行证明.
1701047671
1701047672
本章中将讲几个深入一些的应用,涉及到映射度与不动点问题.
1701047673
1701047674
基础拓扑学讲义 [:1701040239]
1701047675
§1 球面自映射的映射度
1701047676
1701047677
1.1 球面自映射的映射度的定义与性质
1701047678
1701047679


1701047680
设f∶Sn→Sn,n≥1.f诱导出f*n∶Hn(Sn)→Hn(Sn).由于f*n决定一个整数k,使得∀α∈Hn(Sn),f*n(α)=kα.称整数k为f的映射度,记作deg(f)①.
1701047681
1701047682
映射度有下列基本性质.
1701047683
1701047684
命题8.1 (1)若f,g:Sn→Sn都连续,则
1701047685
1701047686


1701047687
deg(gf)=deg(g)·deg(f);
1701047688
1701047689

